STGであたり判定どうやるのか考えてみた その1
STGであたり判定どうやるのか考えてみた その1
本当はDirect~~を使うと便利だと思うし、ベクトルとかで計算もできるはずですけど、そこまでやらずに、円の方程式と媒介変数使ってやってみたいと思います。
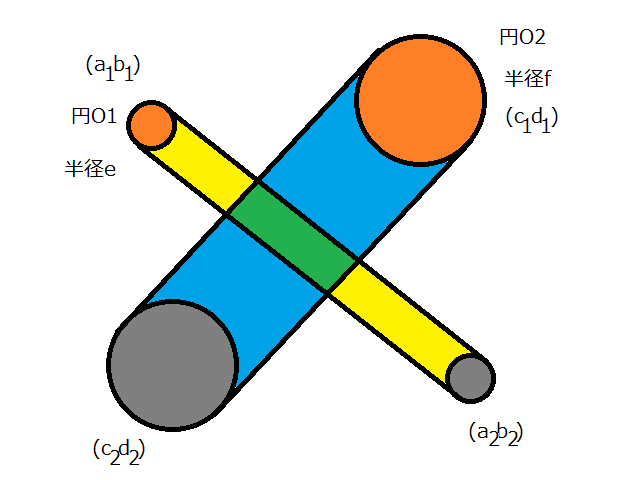
円Oの1と円Oの2があったとします。それぞれの円の中心と半径を(a,b) (c,d) e f とします。
普通に考えると、円同士の距離であたり判定できるので三平方の定理を利用し
(※以下は数学的な書き方をしています。プログラミングのビット演算とかではないのでご注意を)
(a-c)^2+(b-d)^2=距離^2
距離<e+f だったら衝突しているので
(a-c)^2+(b-d)^2<(e+f)^2 の時衝突
ところが、実際はパラパラマンガのように表示しているため、移動スピードが速すぎるとこのままだと通過してしまう可能性があります。
そこで、媒介変数を使って通貨途中のあたり判定もやってしまいます。(以下は眠い中ちゃちゃっとやった計算なので途中で間違ってるかもしれません…。間違ってたら報告お願いします。すいません…。)
動く前と動いた後の座標をそれぞれ
a1,b1,c1,d1
a2,b2,c2,d2
と表すことにする。 (円O1が(a1,b1)から(a2,b2)に移動するという感じ)
tを媒介変数にして0以上1以下の数値が入るとする。
すると円O1の中心の座標が
(t(a2-a1)+a1,t(b2-b1)+b1)
円O2の中心の座標が
(t(c2-c1)+c1,t(d2-d1)+d1)
となる。
そして、これらの値をさっきのように普通に三平方の定理で判定するような式を立てると
[{t(a2-a1)+a1}-{t(c2-c1)+c1}]^2+[{t(b2-b1)+b1}-{t(d2-d1)+d1}]^2
={t(a2-a1-c2+c1)+(a1-c1)}^2+{t(b2-b1-d2+d1)+(b1-d1)}^2
=t^2{(a2-a1-c2+c1)^2+(b2-b1-d2+d1)^2}+2t{(a2-a1-c2+c1)(a1-c1)+(b2-b1-d2+d1)(b1-d1)}+{(a1-c1)^2+(b1-d1)^2}<(e+f)^2
非常に計算がややこしくなるので以下のようにおきます
A=a1-c1 (動く前のX座標の差)
B=b1-d1 (動く前のY座標の差)
C=a2-c2 (動いた後のX座標の差)
D=b2-d2 (動いた後のY座標の差)
E=e+f (半径の合計)
t^2{(C-A)^2+(D-B)^2}+2t{(C-A)A+(D-B)B}+(A^2+B^2-E^2)<0 (0<=t<=1)
これでtに関する不等式ができました。
tが0~1のいずれかの時にちょっとでもこの条件を満たしたら衝突していることになります。
次に判別式を出してみます。
b^2-4acのbの部分が、なんらかの2倍の数値になっているので (2t~~より) 判別式/4 を使います。(式中のDとまざりそうだったのであえて日本語で書きました)
判別式/4={(C-A)A+(D-B)B}^2-{(C-A)^2+(D-B)^2}(A^2+B^2-E^2)
={(C-A)^2A^2+2(C-A)(D-B)AB+(D-B)^2B^2}-{(C-A)^2A^2+(C-A)^2B^2-(C-A)^2E^2+(D-B)^2A^2+(D-B)^2B^2-(D-B)^2E^2}
まったく同じ数が含まれているので消します。
=2(C-A)(D-B)AB-(C-A)^2B^2-(D-B)^2A^2+(C-A)^2E^2+(D-B)^2E^2
ここで一回式全部(-1)倍します
(C-A)^2B^2-2(C-A)B(D-B)A+(D-B)^2A^2-E^2{(C-A)^2+(D-B)^2}
はじめの部分を因数分解します
={(C-A)B-(D-B)A}^2-E^2{(C-A)^2+(D-B)^2}
始めの部分だけ一時的に展開すると一部文字が消えます。
=(CB-AD)^2-E^2{(C-A)^2+(D-B)^2}
ここで(-1)倍して戻します。
E^2{(C-A)^2+(D-B)^2}-(CB-AD)^2
これが判別式です。展開してちゃんと整理してもいいですけど、面倒くさいんでこのまま放置にします。
あとは判別氏にの値によってtが解無しか、重解だから0未満はないということになるか、2つの実数解だから最大と最少を求めてそれが0~1にあったら衝突、とすればよいと思います。
計算間違ってたらやだなー…。
では今回はこの辺で。
↓クリックしてほしい系です。
追加
私の計算が間違っていなければ、
E^2{(C-A)^2+(D-B)^2}-(CB-AD)^2が0より大きく、
-{(C-A)A+(D-B)B}-√[E^2{(C-A)^2+(D-B)^2}-(CB-AD)^2]が0より大きいか-{(C-A)A+(D-B)B}+√[E^2{(C-A)^2+(D-B)^2}-(CB-AD)^2]が1より小さいとき
に衝突しているはずです。
- さらに追加 -
不等式はたぶんあってます。上の「追加」の内容がたぶん間違ってます…。すいません…。もう一度考えてみます。
俺は、面倒くさいから別画面に模擬画面作って色判定w
誰でも一度は考えるその方法ww
でも、画像って案外コピーしたりするの重いですからできるならやめたほうがいいです。
色判定だと、一瞬しかあたり判定してないのと同様に"通り抜け"が起きる可能性がありますので。(簡単に言うと紫が来まs(ry
当たり判定を四角形でやると、判定式の計算が結構簡単だったりするw
四角形ですか…。
たしかにX座標とY座標で端を確認すればできるので、これも媒介変数使えば円より簡単になりそうですね。
でも、東方みたいなのを作りたいと思っているので円同士でやりたいと思います。(できるかわかりませんけど…。)
fmfm
隙間を埋めればいいわけだw
ちょいかんがえてくるわww
物は考え方だ、うん
ケルパニさん電子回路とか向いてるんじゃないですか?
これほどの計算ようやりましたね@@
しっかり全部見ていませんが、やり方は問題なさそうな感じです。
矩形でやるよりは断然作りやすいでしょう。よく思いつきましたね^^!
展開して消える項がたくさんあるならばした方が良いですが、そのままで良いと思います。
あんまりにも長い式になると、計算が負荷になります。
{(C-A)A+(D-B)B}とか、似た計算は部分部分を変数に入れて使い回しした方が速度向上するでしょう。
うはwww
頑張りましたねぇ
でも、四角でもいいんじゃないですか?
円O1の移動前と移動後に仮想の線を引き、その上に一定間隔で仮想の四角形Aをおく。
同様に、円O2にも仮想の四角形Bをおく。
仮想の四角形A,B同士が重なっていないかどうかの判定をすれば終了。
整数演算のみで正確に直線を引くアルゴリズムもありますし、それを組み合わせれば・・・
この記事にあるものよりは遅くなるかと思いますが、こっちの方が理解はしやすいはず。
>橙さん
間を埋めるように塗りつぶしたりしたら余計に重くなりますよw まあどうしても色で判断したいなら仕方ありませんが。できたら数値で…。
>フェルミウム湾さん
実は、計算自体は苦手なんです…orz
計算問題のほうが応用問題よりミスったり、応用問題の最後の足し算でミスるという…。
でもまあ今回の場合は自分でSTG作るために頑張って計算しました。
私はやり方を考える系が特に好きなんです。
で、この間フェルミウム湾さんに媒介変数教えてもらって、「これ、弾幕の並び自体以外に、弾の移動にも使えるじゃん」
ってことで思いつきました。
そうですね、もうちょっと式の置き換えを利用してまとめていったほうがやりやすいですね。実際にプログラムに書くときはそうします。
アドバイスありがとうございます!
そうだ!
画面の点を全て配列変数に置き換えよう!
どこの数に代入するかをあらかじめ設定しておいて…
それなら表示する点なのか違うのかを示すフラグを準備しておくといいですよ。
二次元配列で。
fmfm
了解!
やってみる!
頑張ってください!!
はじめまして
媒介変数いいですよね。
私もネットで知り点同士の当たり判定で計算してたのですがわからいことがあったのですが、
この球体の処理の球体の半径を0にしたらいけますか?
よろしくお願いします。